Translating solutions for Gauß curvature flows with Neumann boundary
condition
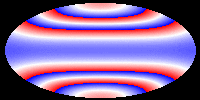
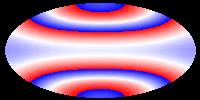
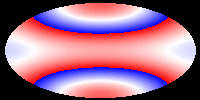
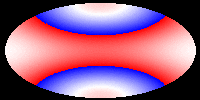
The following pictures and the movie show the velocity of the hypersurface
at different times during the evolution. Colors correspond to velocities,
but the mapping (v -> c) is not injective and only continuous, if blue
and red are identified. These pictures show that during the evolution,
the differences of the velocities at different points of the hypersurface
decrease. Eventually, the hypersurface converges to a hypersurface that
moves with constant speed. This corresponds to the fact that the color
in the picture becomes the same everywhere. In our first movie we show
the beginning of this process, in a second we show the behavior during
a longer time interval.
A run of both movies should take approximately 10 seconds.
t = 0.00 ... 0.25 and 0.00 ... 1.25:
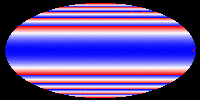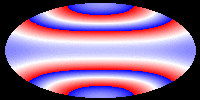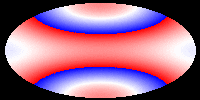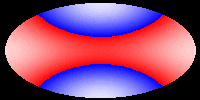
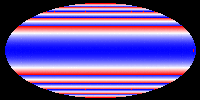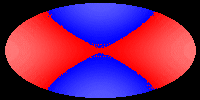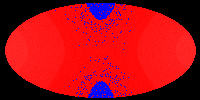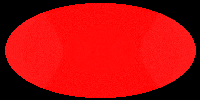
The following pictures show the evolution at t = 0.00, 0.05, 0.10, 0.15,
0.20, and 0.25.


Technical data for the simulation
Our simulation takes place on a 200x100 grid, that is exactly the area
you see on the pictures. This corresponds to [-1,1]x[-0.5,0.5]
in R2. Let E={(x,y) in R2: 1.1 (x2
+(2y)2)<1} and u0=1.5 x2+y2
-0.1 y4. We simulate the flow equation
ut=log det D2u in E subject to the boundary
condition that the normal derivative of u coincides with that of
u0 and the initial condition that u and u0
coincide at time t=0.









