Alberto Passuello (University of Bordeaux)

(Gast von Cordian Riener)

Bounds in network coding from the Semidefinite Programming method

Abstract: Recently, network coding arose as an area of interest in information theory. The codes which are used in this framework come from projective geometry over finite fields, and can be seen as the q-analogs of the classic codes in the Hamming space, but with several differences as well. Therefore, even for such "projective codes" it is possible to apply tools from combinatorial optimization (Linear Programming and Semidefinite Programming) in order to bound their maximal cardinality. I will introduce the subject and explain advantages and limits of the Semidefinite Programming approach in this space.

Montag, 23.04.2012 um 15.15 Uhr, Oberseminar Modelltheorie

kein Vortrag

Montag, 30.04.2012 um 15.15 Uhr, Oberseminar Modelltheorie

kein Vortrag

Freitag, 04.05.2012 um 13.30 Uhr, Oberseminar Reelle Geometrie und Algebra

Peter Bruin (Universität Zürich)

(Gast von Arno Fehm)

Ranks of elliptic curves over number fields with prescribed torsion

http://cms.uni-konstanz.de/math/schwerpunkt-reelle-geometrie-und-algebra/vortraege-im-ss-2012-abstracts/#0405Abstract: Let d be a positive integer, and let T_d be the set of isomorphism classes of groups occurring as the torsion subgroup of E(K), where K is a number field of degree d and E is an elliptic curve over K. It is known that T_d is finite. The sets T_1 and T_2 are known, as well as the subsets of T_3 and T_4 consisting of torsion groups occurring for infinitely many E/K up to isomorphism.

We study the following problem: for d ≤ 4 and T in T_d, what are the possibilities for the rank of E(K) if K is a number field of degree d and E is an elliptic curve over K with torsion group T? In the cases d = 2 and T = Z/13Z, d = 2 and T = Z/18Z, and d = 4 and T = Z/22Z, it turns out that the rank is always even. We explain this by a phenomenon that we call false complex multiplication. This is joint work with Johan Bosman, Andrej Dujella and Filip Najman.

Montag, 07.05.2012 um 15.15 Uhr, Oberseminar Modelltheorie

Yimu Yin (Paris 6)

(Gast von Arno Fehm)

Motivic integration in real closed fields

Abstract: I will describe how to construct Hrushovski-Kazhdan style integration in real closed fields. The setting is based on early work by van den Dries-Lewenberg on T-convex theories. If time permits (most likely not), I will also sketch a potential application to real Milnor fibers.

Freitag, 11.05.2012 um 13.30 Uhr, Oberseminar Reelle Geometrie und Algebra

Patrick Speissegger (McMaster University, Canada)

(Gast von Salma Kuhlmann)

Generating the pfaffian closure with total pfaffian functions

Abstract: Given an o-minimal expansion R of the real field, Gareth Jones and I show that the structure obtained from R by iterating the operation of adding all total Pfaffian functions over R defines the same sets as the Pfaffian closure of R. I will recall the definition of the pfaffian closure of an o-minimal structure and compare this new description of it to other known ones. The talk will be mostly a survey emphasizing the distinctions between the various pfaffian notions, and I will explain how it all comes down to a local problem concerning nested differential forms.

Freitag, 18.05.2012 um 13.30 Uhr, Oberseminar Reelle Geometrie und Algebra

kein Vortrag

Montag, 21.05.2012 um 15.15 Uhr, Oberseminar Modelltheorie

Philipp Hieronymi (University of Illinois, Urbana-Champaign)

(Gast von Salma Kuhlmann)

Interpreting the projective hierarchy in expansions of the real line

Abstract: We give a criterion when an expansion of the ordered set of real numbers defines the image of the expansion of the real field by the set of natural numbers under a semialgebraic injection. In particular, we show that for a non-quadratic irrational number a, the expansion of the ordered Q(a)-vector space of real numbers by the set of natural numbers defines multiplication on the real numbers. This is joint work with Michael Tychonievich (Ohio State).

Donnerstag, 24.05.2012 um 17.00 Uhr, Schwerpunktskolloquium Reelle Geometrie und Algebra

Prof. Petter Brändén (KTH Stockholm)

(Gast von Daniel Plaumann)

On hyperbolicity cones and spectrahedra

Abstract: A major open question in hyperbolic programming is whether all hyperbolicity cones are spectrahedral, that is, if they are slices of the cone of positive semidefinite matrices. We will use combinatorial methods to answer some questions related to the above question.

Freitag, 01.06.2012 um 13.30 Uhr, Oberseminar Reelle Geometrie und Algebra

Philipp Renner (Universität Zürich)

(Gast von Cordian Riener)

Computing Generalized Nash Equilibria by Polynomial Programming

Abstract: We present a new way to solve generalized Nash equilibrium problems, a very useful model in engineering and economics. We assume the feasible set to be closed and compact. Furthermore all functions are assumed to be polynomials. However we do not need any convexity assumptions on either the utility functions or the action sets. The key idea is to use Putinar’s Positivstellensatz to replace each agent’s problem by a convex relaxation. Thus we obtain a system of polynomial equations and inequalities. The solutions to this are all within epsilon of being optimal. In many situations epsilon is zero.

 

Montag, 04.06.2012 um 15.15 Uhr, Oberseminar Modelltheorie

Karen Lange (Wellesley College)

(Gast von Salma Kuhlmann)

Degrees of orderings on torsion-free abelian groups

Abstract: It is well known that an abelian group admits an ordering if and only if it is torsion-free.  This classical statement is false, however, from a computable perspective.  Downey and Kurtz (1986) showed that there is a computable torsion-free abelian group that admits no computable ordering.  We look at generalizations of this result by examining the collection of orderings X(G) on a given computable torsion-free group G.  Specifically, we are interested in the degree spectrum of X(G), i.e., the   set of  degrees of orderings in X(G). One  way to construct orderings is to use a basis for G, and this relationship between bases and orderings has consequences for the degree spectrum of X(G).  Given these consequences, it is natural to ask whether the  degree spectra of orderings on computable torsion-free  abelian groups are  closed upward.  In joint work with Kach and Solomon, we show the answer is no.

Freitag, 08.06.2012 um 13.30 Uhr, Oberseminar Reelle Geometrie und Algebra

Sebastian Petersen (Kassel)

(Gast von Arno Fehm)

Independence of l-adic Galois representations over function fields (Joint work with Gebhard Böckle and Wojciech Gajda)

Abstract: Let K be a field. For every rational prime l let ρ_l : Gal_K → Γ_l be a homomorphism into a group Γ_l and consider the induced homomorphism

ρ : Gal_K → _lΓ_l, σ 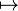(ρ_l(σ))_l.

Following Serre we call the family (ρ_l)_l of homomorphisms almost independent if there exists a finite separable extension E/K such that ρ(Gal_E) = _lρ_l(Gal_E).
Important examples of such families are given by the representations ρ_A,_l : Gal_K → Aut(T_lA) of Gal_K on the l-adic Tate modules of an abelian variety A over K. By a classical theorem of Serre the family (ρ_A,l)_l is almost independent for every abelian variety A over a number field K. A recent preprint of Serre proves an analogous result for families of representations of Gal_K afforded by the l-adic  étale cohomology groups of an arbitrary separated algebraic scheme X over a number field K. Serre, Illusie and Jarden asked whether these results can be extended to the case of a ground field K which is a finitely generated extension of Q of transcendence degree trdeg(K/Q) ≥ 1. In brief: We answer this question affirmatively. Further- more we have results in the case of a finitely generated ground field K of positive characteristic. (Be aware; the most direct analogue is false in positive characteristic already in the case of abelian varieties.)

Montag, 11.06.2012 um 15.15 Uhr, Oberseminar Modelltheorie

kein Vortrag

Freitag, 15.06.2012 um 13.30 Uhr, Oberseminar Reelle Geometrie und Algebra

Danielle  Gondard-Cozette (Institut Mathematique de Jussieu, Universite Paris 6 (Universite Pierre et Marie Curie))

(Gast von Salma Kuhlmann)

An Artin’s theorem for symmetric matrices

Abstract: The talk goes back to an old paper written with Paulo Ribenboim (Bull. Sc. Math. 98 pp. 49-56 (1974)) recently quoted by several authors, including Konrad Schmudgen, Yurii Savchuk and Jaka Cimpric, in papers dealing with non commutative real algebraic geometry.
We provide an Artin’s theorem for positive definite symmetric matrices having entries in the rational function field with several variables over a real closed field.

Montag, 18.06.2012 um 15.15 Uhr, Oberseminar Modelltheorie

Danielle  Gondard-Cozette (Institut Mathematique de Jussieu, Universite Paris 6 (Universite Pierre et Marie Curie))

(Gast von Salma Kuhlmann)

On some elementary field theories

Abstract: Orderings have very nice links with valuations and we provide some back- ground on relations between orderings and valuations. But in a formally real field one can also consider objects more general than orderings, which also have a close relationship with valuations: these are called valuation fans. We introduce valuation fans and give some examples.
Then, field theories related to valuation fans are introduced. These are related to valuation fans in the same way that real closed fields are related to orderings. Doing this we get elementary field theories with nice first order axiomatizations and finally study these theories.

 

Freitag, 22.06.2012 um 13.30 Uhr, Oberseminar Reelle Geometrie und Algebra

Maria Charina (TU Dortmund)

(Gast von Claus Scheiderer)

Algebra and optimization for signal and image processing

Abstract: In this talk we show that, on one hand, the existence of certain families of functions used in signal and image processing is related to the existence of sums of squares decompositions of certain nonnegative trigonometric polynomials. On the other hand, the existence of such families of functions is also related to the solvability of certain problems of semi-definite programming. We illustrate the result we present with several examples.
This is a joint work with Claus Scheiderer, University of Konstanz, Mihai Putinar, University of Santa Barbara and Joachim Stöckler, TU Dortmund.

Montag, 25.06.2012 um 15.15 Uhr, Oberseminar Modelltheorie

Katharina Dupont (Konstanz)

Definable Valuations and Dependent Fields

Abstract: For my PhD project I am working on definable valuations on dependent fields.
Our aim is to find necessary and sufficient (algebraic or model theoretic) conditions for dependent fields to admit a definable valuation.
In the first part of my talk I will give an introduction to dependent fields. I will give a definition and several theorems which help us to decide whether a given field is dependent. I will talk about the main ideas of how these theorems are used to show that finite fields, algebraically closed fields, real closed fields, $\Q_p$ for any prime $p$ and almost real closed fields are dependent fields. I will as well shortly talk about definable valuations on these fields.
In the second part of my talk I will present a promising method which uses definable subgroups to find definable valuations on fields.

Donnerstag, 28.06.2012 um 17.00 Uhr, Schwerpunktskolloquium Reelle Geometrie und Algebra

Prof. Karl Strambach (Universität Erlangen-Nürnberg)

(Gast von Claus Scheiderer)

Imprimitive Transformationsgruppen, die auf den Blöcken scharf 2-fach transitiv operieren

Abstract: Die Klasse der scharf zweifach transitiven Gruppen verallgemeinert in natürlicher Weise die Klasse der affinen Abbildungen einer Geraden über einem Körper; sie wird seit der Klassifikation der endlichen scharf zweifach transitiven Gruppen durch Zassenhaus 1936 intensiv studiert. Im Vortrag will ich die Klasse der (2, 2)-Transformationsgruppen vorstellen, die in ähnlicher Weise die Klasse der affinen Abbildungen einer Geraden über einem Ring der dualen Zahlen verallgemei- nern. Die (2, 2)-Transformationsgruppen sind imprimitiv; daher ist ihre Axiomatik natürlich komplizierter als die von scharf zweifach transitiven Gruppen, die primitiv sind. Da eine (2, 2)- Transformationsgruppe auf der Menge der Blöcke scharf zweifach transitiv wirkt, ist für eine Klassifikation von (2, 2)-Transformationsgruppen die Kenntnis der scharf zweifach transitiven Gruppen unentbehrlich. So wie die Fastkörper bei Zassenhaus spielen bei Untersuchungen von (2,2)-Transformations-gruppen die paradualen Fastringe eine entscheidende Rolle.

 

Freitag, 29.06.2012 um 13.30 Uhr, Oberseminar Reelle Geometrie und Algebra

Michael Junk (Konstanz)

(Gast von Claus Scheiderer)

Maximum Entropy Moment Problems

Abstract: In the talk, I will introduce research projects in the area of computational gas dynamics, semiconductor simulation, and material science where finite moment problems play a central role. In each of these projects, the maximum entropy approach is used to construct specific solutions and the main part of the talk will be devoted to the formulation of general solvability conditions which cover the specific problems.

Montag, 02.07.2012 um 15.15 Uhr, Oberseminar Modelltheorie

Assaf Hasson (Ben-Gurion University of the Negev, Israel)

(Gast von Salma Kuhlmann)

Geometric structures interpretable in o-minimal theories

Abstract: In the 70s of the 20th century Zilber conjectured that if the geometry of a strongly minimal set is not locally modular then the geometric complexity of the structure must arise from an algebraic complexity, namely the existence of an infinite definable field. Though, Zilber's conjecture is far from being true it has been proved - and even generalised - in many special cases of "tame" geometric structures, with far reaching consequences. In 2004 Peterzil asked whether Zilber's conjecture must hold of geometric structures interpretable in o-minimal theories (the question is still open even for the special cases of structures interpretable in compact complex manifolds or even in algebraically closed fields of characteristic 0). This is, probably, the widest general context in which no counter examples are known.
In the talk - beside explaining the different notions needed for the discussion - I will give an overview of the state of the art regarding Peterzil's question, sketching the solution for the unstable case, and discussing the prospects with regard to the stable case.

Donnerstag, 05.07.2012 um 17.00 Uhr, Schwerpunktskolloquium Reelle Geometrie und Algebra

Prof. Colm Mulcahy (Spelman College, Atlanta, Georgia)

(Gast von Claus Scheiderer)

Celebration of Mind: The Mathematics, Magic \& Mystery of Martin Gardner

Abstract: Martin Gardner, Prince of Recreational Mathematics, died in May 2010 after an astonishing publishing career spanning 80 years. His "Mathematical Games" column in Scientific American ran from the 1950s to the 1980s, and introduced thousands of budding mathematicians to elegant problems and magical items which still inspire "Aha!" moments today. We'll survey some of what "the best friend mathematics ever had" achieved and the legacy he leaves behind.

Freitag, 06.07.2012 um 13.30 Uhr, Oberseminar Reelle Geometrie und Algebra

Victoria Powers (Emory University)

(Gast von Claus Scheiderer)

Pólya's Theorem with Zeros.

Abstract: Joint work with M. Castle and B. Reznick. Let R[X] = R[X_1, … , X_n]. Pólya's Theorem says that if a form (homogeneous polynomial) p in R[X] is positive on the standard simple in R^n, then for sufficiently large N all the coefficients of (X_1 + … + X_n)^N times p are positive. In 2001, Powers and Reznick gave a bound on the N needed, in terms of the degree of p, the size of the coefficients, and the minimum of p of the simplex. This result has been used in many applications, in both pure and applied math. In this talk, we extend the quantitative Pólya's Theorem to forms which are allowed to have zeros on the simplex. We give a complete characterization of forms which are Pólya semi-positive, i.e., forms for which the conclusion of the theorem holds with "positive coefficients" relaxed to "nonnegative coefficients". We discuss an application to representations of polynomials nonnegative on compact polyhedra.

Montag, 09.07.2012 um 15.15 Uhr, Oberseminar Modelltheorie

Zoe Chatzidakis (CNRS - University Paris 7)

(Gast von Salma Kuhlmann)

Algebraic dynamics, difference fields and model theory

Abstract: (Joint work with E. Hrushovski).
M. Baker proved in 2007 that given a endomorphism f of P^1 of degree >1 and defined over a function field K, either all points of P^1(K) of canonical height 0 are preperiodic, or the endomorphism f descends to the field of constants of K. Szpiro and Tucker asked about generalising the result to higher dimensional varieties. A reformulation by Szpiro of the hypotheses in terms of limited sets allowed model theory to get into the picture, more precisely the model theory of difference fields. We were therefore able to give the correct formulation of the descent result in higher dimension, and prove it.
This is what I will explain in the talk: connections between algebraic dynamics and difference fields; translation of the problem; how model theory of difference fields intervenes.

Freitag, 13.07.2012 um 13.30 Uhr, Oberseminar Reelle Geometrie und Algebra

Andrew Obus (Max-Planck-Institut für Mathematik, Bonn)

(Gast von Arno Fehm)

The Oort conjecture on lifting covers of curves

Abstract: The lifting problem states: Given a curve in characteristic p and a cyclic group of automorphisms, when can one lift the curve, together with the group of automorphisms, to characteristic zero? Frans Oort conjectured that this should be possible when the group of automorphisms is cyclic. This conjecture has recently been proved by the speaker, Stefan Wewers, and Florian Pop. I will give a large amount of background on the problem before outlining the proof. The last part of the proof (the work of Pop) uses (basic) model theory, and I will try to give some details on this. No background in model theory will be required.

Montag, 16.07.2012 um 15.15 Uhr, Oberseminar Modelltheorie

kein Vortrag

Donnerstag, 19.07.2012 um 17.00 Uhr, Mathematisches Kolloquium

Dr. Peter Schuster (University of Leeds)

(Gast von Karim Johannes Becher)

Eine Verallgemeinerung des Lemmas von Krull

Abstract: Manch ein vermöge des Zornschen Lemmas geführter, indirekter Beweis konnte bereits in einen direkten Beweis mit Hilfe des von Raoult formulierten Prinzips der Offenen Induktion umgewandelt werden. In hinreichend konkreten Situationen kann man dabei auch einen konstruktiven Beweis völlig ohne Auswahlaxiom erhalten. Um nunmehr den Boden für eine systematischere Behandlung zu bereiten, ordnen wir die in der mathematischen Praxis vorkommenden Instanzen des Zornschen Lemmas in repräsentative Beweismuster ein. Beispielsweise umfaßt eine Verallgemeinerung des Lemmas von Krull nicht nur Beweistechniken aus verschiedenen Sparten der Algebra, sondern auch einen Vollständigkeitsbeweis à la Henkin für nicht notwendig abzählbare Sprachen der erststufigen Logik.

Freitag, 20.07.2012 um 13.30 Uhr, Oberseminar Reelle Geometrie und Algebra