Jeder mathematische Text benötigt einem Kontext, um gelesen und verstanden werden zu können. Der Kontext besteht dabei aus einer Liste von Symbolen und Objektbezeichnungen, für die bereits eine Bedeutung vereinbart wurde, sowie aus einer Liste der bereits geltenden Aussagen. Umgekehrt hat der mathematische Text eine verändernde Wirkung auf den Kontext.

Stehen beispielsweise die Symbole \(x\) und \(y\) in einem  Kontext für reelle Zahlen, dann können wir ihrem arithmetischen Mittelwert \((x+y)/2\) den Namen \(a\) geben, sofern dieser im betrachteten Kontext noch keine Bedeutung trägt. Durch diese Namensvereinbarung wächst der Vorrat an belegten Objektbezeichnungen, was einer Kontextänderung entspricht. Die Änderung wird dabei mit dem Definitionssymbol \(:=\) signalisiert, indem wir \(a:=(x+y)/2\) schreiben. Nach diesem Schritt kann der Name \(a\) in weiteren Ausdrücken verwendet werden, wobei er wie die Zahlzeichenketten einen Grundausdruck darstellt.

Der Zeichenvorrat für Namen ist durch die üblichen lateinischen Buchstaben \(a,b,c,\ldots\) gegeben, wobei zwischen Groß- und Kleinbuchstaben unterschieden wird. Außerdem sind Zeichen anderer Alphabete gebräuchlich wie griechische \(\alpha,\beta,\gamma,\ldots\) oder hebräische \(\aleph,\beth,\gimel\). Genügen diese Möglichkeiten nicht oder werden sie zu verwirrend, ist es auch möglich, Zeichenketten als Namen zu verwenden. Auch wenn diese dann wie Wörter der Umgangssprache erscheinen, darf man nicht vergessen, dass sich ihre Bedeutung allein aus dem präzisen Objektausdruck auf der rechten Seite des Definitionssymbols ergibt und nicht aus der umgangssprachlichen Bedeutung (auch wenn diese sich sinnvollerweise ähneln).  

Werden durch den mathematischen Text neue Aussagen bewiesen, so wächst die Liste der geltenden Aussagen und der Kontext ändert sich ebenfalls. Dieser Aspekt liegt allerdings hier nicht im Fokus.

Für das Lesen und Schreiben sehr wichtig ist die Beobachtung, dass Kontexte ineinander verschachtelt auftreten. Zum Beispiel formt jeder mathematische Satz einen neuen Kontext, in dem die bereits vorhandenen Namen und geltenden Aussagen durch weitere Objektnamen und  Satzvoraussetzungen ergänzt werden. Um die Verwaltung der Namen genauer zu beschreiben, benutzen wir hier eine schematische Darstellung, in der Kontexte durch rechteckige Kästen dargestellt werden. Ein Kasten in einem anderen Kasten ist dann ein Unterkontext.

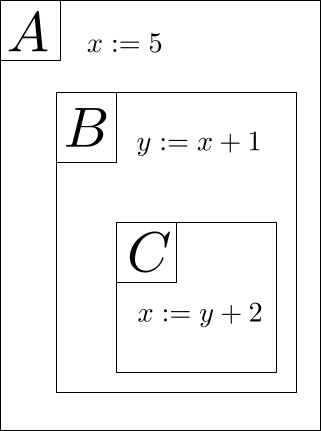
In diesem Beispiel wird im Kontext \(A\) der Name \(x\) für die Zahl \(5\) eingeführt. Im Unterkontext \(B\) steht dieser Name dann zur Verfügung und wird zur Definition von \(y\) verwendet (\(y\) hat hier also den Wert \(6\)). Entsprechend vererbt sich der Name \(y\) in den Unterkontext \(C\), während er außerhalb von \(B\) nicht verwendet werden kann. Eine Besonderheit ergibt sich im Kontext \(C\). Hier erhält der Name \(x\) mit dem Wert \(8\) eine neue Bedeutung, die den Wert \(5\) aus Kontext \(A\) überdeckt. Während im gleichen Kontext Bedeutungswechsel von Namen nicht erlaubt sind, ist eine Neubelegung eines bereits vergebenen Namens über Kontextgrenzen hinweg dennoch möglich. Bei weiterer Vererbung der Namen gilt immer die zuletzt zugewiesene Bedeutung. 

Das Betreten eines neuen Kontextes wird im Text oft durch die Wortgruppe Seien ... gegeben und es gelte ... eingeleitet. Ebenso gibt es charakteristische Wendungen oder Symbole für das Schließen von Kontexten (in Beweisen wird zum Beispiel oft qed notiert als Abkürzung für quod erat demonstrandum - was zu beweisen war). Das verschachtelte Auftreten von gedanklichen Umgebungen ist übrigens nicht auf mathematische Texte beschränkt. Auch in Romanen können Geschichten innerhalb der eigentlichen Geschichte erzählt werden oder Texte in Zeitschriften werden von Infoboxen unterbrochen und anschließend fortgesetzt. Typisch für mathematische Texte ist aber, dass die Schachtelung sehr häufig und auch über viele Ebenen hinweg auftritt.

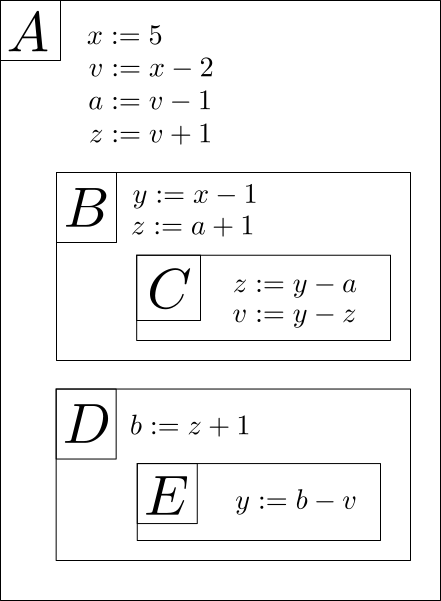
In der folgenden Übung soll die wichtige Buchhaltung von benutzbaren Namen und den zugehörigen Bedeutungen zumindest schematisch geübt werden. Grundlage dazu ist das folgende Kontext-Diagramm.