Brotkrumen-Navigation
Aussagenlogik
Im Abschnitt über Kontexte wurde erwähnt, dass das gedankliche Führen einer Liste geltender Aussagen sehr wichtig zum Lesen und Schreiben eines mathematischen Textes ist. Aber was ist mit den Aussagen die nicht gelten? Dass hierfür keine eigene Liste notwendig ist, ergibt sich aus folgendem Trick: Wenn wir uns merken wollen, dass eine Aussage \(E\) falsch ist, dann tragen wir einfach "\(E\) ist falsch" in die Liste der geltenden Aussagen ein. Als Abkürzung hierfür wird das Symbol \(\neg\) der Aussage \(E\) vorangestellt, d.h. \(\neg E\) in der Liste der geltenden Aussagen bedeutet, dass \(E\) nicht gilt (aus diesem Grund wird \(\neg\) beim Lesen als "nicht" ausgesprochen und wir nennen Aussagen der Form \(\neg E\) auch Negationen).
Das Symbol \(\neg\) eröffnet uns die Möglichkeit, eine Aussage \(E\) in ihre gegenteilige Aussage \(\neg E\) zu verwandeln. Allgemein sprechen wir bei einer solchen Schreibweise von einem Präfix-Ausdruck. Umgekehrt gibt es auch die Möglichkeit durch ein nachfolgendes Symbol einen Ausdruck zu modifizieren. Diese Konstellation nennt man einen Postfix-Ausdruck.
Bei einem Präfix-Ausdruck steht ein Symbol vor einem Grundausdruck oder einem Klammerausdruck. Bei einem Postfix-Ausdruck steht das Symbol hinter einem Grundausdruck oder einem Klammerausdruck.
Neben dem Negieren einer Aussage gibt es verschiedene Aussagenverknüpfungen, die durch Infix-Ausdrücke symbolisiert werden. Um sie einzeln vorzustellen, seien \(E\) und \(F\) jeweils Platzhalter für Aussagenausdrücke. Die Bedeutung der daraus gebildeten Aussagen-Verknüpfungen ergibt sich aus den Regelungen rund um deren Gelten. Da die Regeln nicht nur für das Beweisen und Argumentieren sondern auch für das Verständnis beim Lesen und Schreiben wichtig sind, wollen wir sie ebenfalls kurz vorstellen.
- Die Konjunktionsaussage \(E\wedge F\) gilt in einem Kontext genau dann, wenn beide Aussagen \(E\) und \(F\) in diesem Kontext getrennt gelten. Ausgesprochen wird \(E\wedge F\) als \(E\) und \(F\), weil die Und-Verknüpfung in der Umgangssprache die gleiche Rolle spielt (denke z.B. an: Die Sonne scheint und die Blumen blühen).
- Die Disjunktionsaussage \(E\vee F\) gilt in einem Kontext genau dann, wenn mindestens eine der beiden Aussagen \(E,F\) in diesem Kontext gelten. Ausgesprochen wird \(E\vee F\) als \(E\) oder \(F\), weil die Oder-Verknüpfung in der Umgangssprache die gleiche Rolle spielen kann (denke z.B. an: Wer Schüler ist oder wer heute Geburtstag hat, bekommt freien Eintritt). Allerdings ist hier etwas Vorsicht geboten, denn in der Umgangssprache gibt es eine zweite Bedeutung der Oder-Verknüpfung (z.B. Als kostenloses Frühstücksgetränk bekommen Sie einen Tee oder Sie bekommen einen Kaffee), bei der das gleichzeitige Gelten der beiden Aussagen von vornherein ausgeschlossen ist. In der Mathematik wird diese Verknüpfung exklusives Oder genannt und nur sehr selten benutzt, so dass sich kein universelles Infix-Zeichen durchgesetzt hat.
- Die Implikationsaussage \(E\Rightarrow F\) gilt in einem Kontext, wenn unter der Annahme, dass \(E\) gilt, auch \(F\) gilt. Ausgesprochen wird \(E\Rightarrow F\) als wenn \(E\) dann \(F\), oder aus \(E\) folgt \(F\), oder auch \(E\) impliziert \(F\), weil die Wenn-Dann-Verknüpfung in der Umgangssprache die gleiche Rolle spielt (denke z.B. an: Wenn es regnet, dann ist die Straße nass).
- Die Äquivalenzaussage \(E\Leftrightarrow F\) gilt in einem Kontext genau dann, wenn \(E\) und \(F\) den gleichen Wahrheitswert besitzen. Ausgesprochen wird \(E\Leftrightarrow F\) als \(E\) genau dann, wenn \(F\), weil die Genau-Dann-Wenn-Verknüpfung in der Umgangssprache die gleiche Rolle spielt (denke z.B. an: Genau dann, wenn die Fußgängerampel grün zeigt, darf ich die Straße dort überqueren).
In der Praxis treten die grundlegenden Aussageverknüpfungen oft verschachtelt auf, so dass Klammerungen notwendig werden. Um die nach unseren Regeln korrekt geklammerten Ausdrücke zu erkennen, hier nochmal eine kleine Übung in der Grundausdrücke (in Form von Platzhalternamen), Klammer-, Infix und jetzt auch Präfix-Ausdrücke auftreten.
Gerade bei sehr verschachtelten Ausdrücken wie \((A\Rightarrow (\neg (B\vee A)))\wedge((B\wedge C) \Leftrightarrow A)\) ist es später beim Beweisen wichtig, dass du schnell erkennst, um welchen Aussagentyp es sich insgesamt handelt, d.h. aus welcher der Grundformen\( \neg E, E\wedge F, E\vee F, E\Rightarrow F\) oder \(E\Leftrightarrow F\) der Ausdruck durch Ersetzen von \(E\) und \(F\) entstanden ist. Im vorliegenden Fall haben wir es zum Beispiel mit einer Und-Aussage zu tun, denn der Ausdruck entsteht aus \(E\wedge F\) wenn wir \(E\) durch \(A\Rightarrow (\neg (B\vee A))\) und \(F\) durch \((B\wedge C) \Leftrightarrow A\) ersetzen.
Die gesamte Struktur des Ausdrucks entsteht durch Wiederholung des Vorgangs mit den Teilausdrücken. So ist der linke Teilausdruck eine Implikation, deren rechter Teilausdruck eine Negation ist usw. Sehr übersichtlich kann man die Gesamtstruktur durch einen sogenannten Ausdrucksbaum darstellen. Für unseren Beispielausdruck sieht dieser so aus:
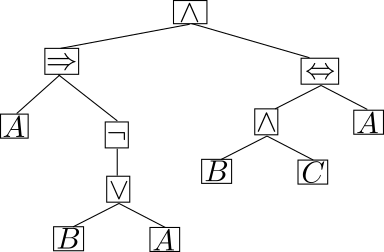
Um welchen Aussagetyp es insgesamt geht kann man in dieser Darstellung leicht am oberen Symbol erkennen (der sogenannten Wurzel des Ausdrucksbaums). Von der Wurzel führen die Zweige auf die beiden Teilausdrücke, deren Ausdruckstyp wieder am dort angegebenen Symbol zu erkennen ist. In den sogenannten Blättern des Baums enden die Verzweigungen. Hier stehen immer Grundausdrücke.
Um die passende Beweisstrategie für eine Aussage zu finden, musst du zuerst ihren Aussagetyp erkennen. Genauso brauchst du den Aussagetyp für die Benutzung einer geltenden Aussage, um auch hier die richtige Strategie auszuwählen.
Als Übung hierzu sollst du in der nächsten Aufgabe den Aussagetyp der rechts stehenden verschachtelten Ausdrücke bestimmen.
 Regeln
Regeln